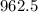Question

A military plane is flying directly toward an air traffic control tower, maintaining an altitude of 12 miles above the tower. Theradar detects that the distance between the plane and the tower is 20 miles and that it is decreasing at a rate of770 mph. What is the ground speed of the plane? Round your answer to two decimal places if necessary.

Answer 1

Consider the following diagram of the situation:

By the Pythagorean theorem, we obtain the following equation:

`d^2=x^2+12^2`

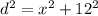
this is equivalent to:

`d^2=x^2+144`

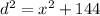
now, when d = 20, we get:

`20^2=x^2+144`

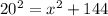
this is equivalent to:

`400=x^2+144`

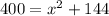
solving for x, we get:

`x^{}=\sqrt[]{400-144}=\text{ }\sqrt[]{256}=16`

On the other hand, consider again the following equation:

`d^2=x^2+144`

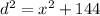
Deriving implicitly, we get:

`2xx^(\prime)=2dd^(\prime)^{}`

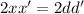
solving for the derivative of x, we get:

`x^(\prime)=(dd^(\prime))/(x)`

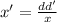
note that in this case, the derivative of d is 770, d=20, and x=16, so :

`x^(\prime)=\frac{(20)(770)^{}}{16}=962.5`

so that, we can conclude that the solution is:

`962.5`