We can see from the graph that we have a conic section in which we have the sum of the distances to two fixed points equals a certain constant.
As we can see from the question, we have:
1. Then we have that for this figure if we have that:
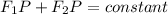
2. In words, we have the sum of the distance from one of the focus, F1, to the point P, and the distance from the focus, F2, to the point P is always constant.
An example of the ellipse is the movement of the planets around the Sun. The planets move around the Sun forming an ellipse, in which the Sun is one of the focus.
We can also say that this figure is a stretched circle, and it is known as Ellipse.
Therefore, in summary, the conic section defined by the set of all points in a plane for which the sum of the distances to two fixed points equals a certain constant is the Ellipse (option A).