Question

Question 7Points 2Find whether the function y =-2x2 - 4x + 7 opens upward or downward. Also, fincwhether it has a maximum or minimum point.

Answer 1

First, let's compare the given equation with the standard form of a quadratic equation, so we can find the parameters a, b and c:

`\begin{gathered} y=ax^2+bx+c\\ \\ y=-2x^2-4x+7\\ \\ a=-2,b=-4,c=7 \end{gathered}`

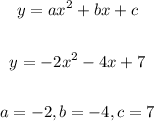
The value of a indicates if the graph opens upward or downward:

a > 0: graph opens upward.

a < 0: graph opens downward.

Since a = -2 is negative, the graph opens downward.

Also, if the graph opens downward, the vertex of the graph is a maximum point.

Therefore the correct option is the third one.