so, we have a angle U=90 degrees it means , that this is a rigth triangle, we can use the Pithagoras theorem
is says
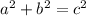
where, a and b are the legs of the triangle and c is the hypotenuse.
Also
TS=41
UT=40
SU=9
so, the longest side is the hypotenuse=TS=41
hypotenuse=41
Leg1=40
Leg2=9
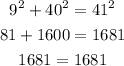
then, it is a rigth triangle, we can use trigonometric relations to find tan S

Now, we have to identify opposite side and adjacen side.
for the angle S, the opposite side is TU=40
and the adjacen side is SU=9
replace the values
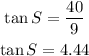
to the nearest hundredth
Tan S=4.44