Question

How would you find the inverse of
`g(x) = \sqrt[3]{x + 1}`

Answer 1

We have the function

`g(x)=\sqrt[3]{x+1}`

and we would like to find the inverse of it.

To do this, first we change the name of the function to y (this way is more easy to manipulate the expression), then

`y=\sqrt[3]{x+1}`

Now we need to solve this equation for x, let's do this.

`\begin{gathered} y=\sqrt[3]{x+1} \\ y^3=(\sqrt[3]{x+1})^3 \\ y^3=x+1 \\ x=y^3-1 \end{gathered}`

Once we do this the x is the inverse function. Now we relabeled the variables, x would be g^(-1) and y will be x.

Therefore

`g^(-1)(x)=x^3-1`

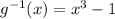
To make sure we are right let's do the composition between the original function and its inverse (we know that the result should be the identity function).

`\begin{gathered} (g\circ g^(-1))(x)=g(g^(-1)(x)) \\ =g(x^3-1) \\ =\sqrt[3]{x^3-1+1} \\ =\sqrt[3]{x^3} \\ =x \end{gathered}`

since this holds, our solution is correct.