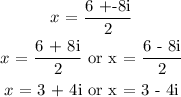The general form of a quadratic equation is expressed as
ax^2 + bx + c
The given equation is
x^2 - 6x + 32 = 7
x^2 - 6x + 32 - 7 = 0
x^2 - 6x + 25 = 0
By comparing with the given equation,
a = 1, b = - 6, c = 25
We would solve the equation by applying the quadratic formula which is expressed as
![x\text{ = }\frac{-b+-\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/vhd3gbghtt8pruo8q6qrympn4y2zc36pw8.png)
We would substitute the given values into the equation. It becomes
![\begin{gathered} x\text{ = }\frac{-\text{ - 6 +-}\sqrt[]{-6^2-4(1*25)}}{2\text{ }*1} \\ x\text{ = }\frac{6+-\sqrt[]{36-100}_{}_{}}{2} \\ x\text{ = }\frac{6\text{ +-}\sqrt[]{-64}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/15tfk4g745oqy863h13cisnyi4izw2jfp5.png)
Recall that the root of a negative number is a complex root. It would be written in form of complex numbers. It becomes