Answer:
Bottles of water: 40
Protein Bars: 20
Step-by-step explanation:
If we call
B = number of protein Bars
W = number of Water bottles
Since each B costs $0.9, each W costs $0.7 and the total spend is $46
We can write the equation:
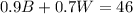
Because, the total of $46 is equal to the number of W times the price, plus the number of B times the price.
We also know that there are twice as many W as B, we can write:
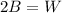
We have these two equations:

We can substitute the second equation in the first one:

Now we can solve:
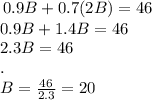
B = 20, means that the amount of protein bars bought is 20.
Now, since there are twice as many bottles of water as protein bars:
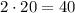
There are 40 water bottles and 20 protein bars