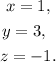1 Answer

EJS · Answer 1 · 2023-08-16T23:21:54+0000

Adding the second and the third equations we get:

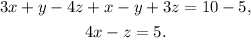
$\begin{gathered} 3x+y-4z+x-y+3z=10-5, \\ 4x-z=5. \end{gathered}$

Now, adding the first and two times the second equation we get:

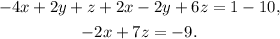
$\begin{gathered} -4x+2y+z+2x-2y+6z=1-10, \\ -2x+7z=-9. \end{gathered}$

Then, we have the following system of equations:

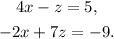
$\begin{gathered} 4x-z=5, \\ -2x+7z=-9. \end{gathered}$

Adding the first equation to two times the second equation, and solving for z we get:

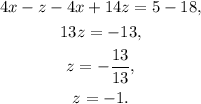
$\begin{gathered} 4x-z-4x+14z=5-18, \\ 13z=-13, \\ z=-(13)/(13), \\ z=-1. \end{gathered}$

Substituting z=-1 in the first equation of the second system and solving for x we get:

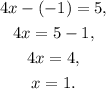
$\begin{gathered} 4x-(-1)=5, \\ 4x=5-1, \\ 4x=4, \\ x=1. \end{gathered}$

Finally, substituting x=1, z=-1, and solving for y in the first equation of the first system we get:

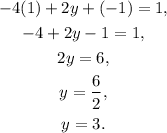
$\begin{gathered} -4(1)+2y+(-1)=1, \\ -4+2y-1=1, \\ 2y=6, \\ y=(6)/(2), \\ y=3. \end{gathered}$

Answer:

$\begin{gathered} x=1, \\ y=3,\text{ } \\ z=-1. \end{gathered}$

Please log in or register to add a comment.