1 Answer

Hessuew · Answer 1 · 2023-09-03T11:20:49+0000

The volume of a sphere can be calculated using this formula:

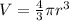
$V=(4)/(3)\pi r^3$

Where "r" is the radius of the sphere and "V" is the volume of the sphere.

If you solve for "r", you get this new formula:

$r=\sqrt[3]{(3V)/(4\pi)}$

In this case you know that:

$V\approx7,238.23\operatorname{mm}^3$

Therefore, you can substitute this value into the second formula and then evaluate, in order to find the radius of this sphere:

$\begin{gathered} r=\sqrt[3]{\frac{(3)(7,238.23\operatorname{mm}^3)}{4\pi}} \\ \\ r\approx12\operatorname{mm} \\ \end{gathered}$

The answer is:

$r\approx12\operatorname{mm}$

Please log in or register to add a comment.