Question

The phone company Splint has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone. If a customer uses 300 minutes, the monthly cost will be $70. If the customer uses 770 minutes, the monthly cost will be $117.A) Find an equation in the form y=mx+b, where x is the number of monthly minutes used and y is the total monthly of the Splint plan. B) Use your equation to find the total monthly cost if 926 minutes are used. If 926 minutes are used, the total cost will be?

Answer 1

Part A:

`y=0.1x+40`

Part B:

The total cost would be $132.6

Explanation:

Part A:

Let x be the minutes spent on the phone that month and y be the monthly cost.

Notice that we'll have two points that belong to the line that models this situation:

`\begin{gathered} (300,70) \\ (770,117) \end{gathered}`

Using these two points, we can calculate the slope of the line as following:

`\begin{gathered} m=(117-70)/(770-300) \\ \\ \Rightarrow m=0.1 \end{gathered}`

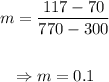
Now, we can use this slope, point (300,70) and the slope-intercept form to get an equation, as following:

`\begin{gathered} y-70=0.1(x-300) \\ \rightarrow y-70=0.1x-30 \\ \\ \Rightarrow y=0.1x+40 \end{gathered}`

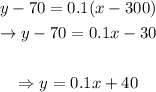
This way, the equation that models the situation is:

`y=0.1x+40`

Part B:

Let's substitute x for 926 in the equation, as following:

`\begin{gathered} y=0.1(926)+40 \\ \\ \Rightarrow y=132.6 \end{gathered}`

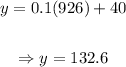
This way, we can conclude that the total cost would be $132.6