Approximately 30.47 units
To find the Perimeter of this polygon, we can find by calculating the distance between each point
Considering the points are:
1 (3,2) R (1,2) (7,7) and (-3,-2)
1) Let's calculate the distance between each of them, using the formula of the distance derived from the Pythagorean Theorem.
d1 = (3,2) and (1,2)
d_2 =(1,2) and (7,7)
d_3= (7,7) and (-3,-2)
d_4= (-3,-2) and (3,2)
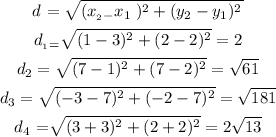
2) Since we have four points then let's consider them as our vertices, and add those line segments do calculate its Perimeter (2P)
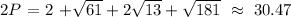
Notice that for those radicals are not perfect squares they are irrational so approximating these we have.