To determine which data set has the smallest standard deviation you have to determine the standard deviation of each sample and then compare them. The standard deviation is the square root of the variance, which means that you have to calculate the variance of each sample and then their standard deviation.
The formula for the sample variance is:
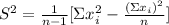
Where
∑xi represents the sum of all observations of the sample
∑xi² represents the sum of the squares of all observations of the sample
n represents the sample size
Sample 1
Variance
n= 10
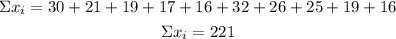
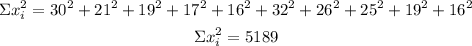
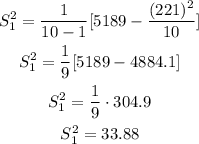
Standard deviation
![\begin{gathered} S_1=\sqrt[]{S^2_1} \\ S_1=\sqrt[]{33.88} \\ S_1=5.82 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4r9zcbhyjrhye3d8wqgb93mjpekze6ty8h.png)
Sample 2
Variance
n=10
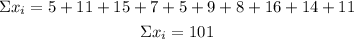
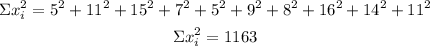
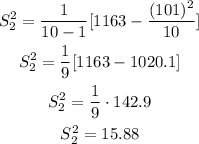
Standard deviation
![\begin{gathered} S_2=\sqrt[]{S^2_2} \\ S_2=\sqrt[]{15.88} \\ S_2=3.98 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bh7c7mcnzr1g7aoyybtc3jq42qy9w8g3kj.png)
Sample 3
Variance
n=10
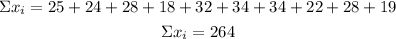
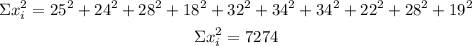
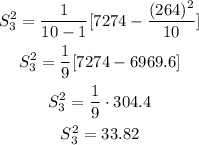
Standard deviation
![\begin{gathered} S_3=\sqrt[]{S^2_3} \\ S_3=\sqrt[]{33.82} \\ S_3=5.82 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8ex5c2cny9sqq10b2jn0ttfn8u82ovcquy.png)
Sample 4
Variance
n=10
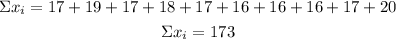
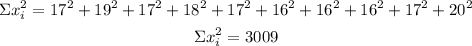
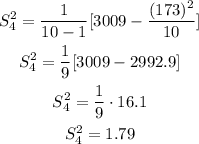
Standard deviation
![\begin{gathered} S_4=\sqrt[]{S^2_4} \\ S_4=\sqrt[]{1.79} \\ S_4=1.34 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/idflvtx99adztfb83i61byvck6v8ehe7ek.png)
Sample 5
Variance
n=10
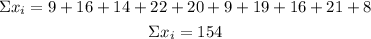
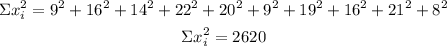
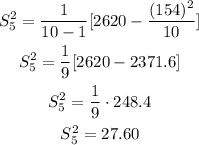
Standard deviation
![\begin{gathered} S_5=\sqrt[]{S^2_5} \\ S_5=\sqrt[]{27.60} \\ S_5=5.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rg07mlvng02xpv24x71l28nlu3sun0himo.png)
So, the standard deviation of the five samples are:
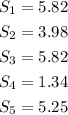
Sample 4 has the smallest standard deviation.