Question

Step 2 of 2: Use the discriminant b ^ 2 - 4ac to determine the number of solutions of the given quadratic equationThen solve the quadratic equation using the tormuisx = (- b plus/minus sqrt(b ^ 2 - 4ac))/(2a)

Answer 1

The value of x is 4

EXPLANATIONS;

Given that

`\text{ -x}^2\text{ = - 8x + 16}`

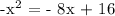
Re-write the quadratic function

`-x^2\text{ + 8x - 16 = 0}`

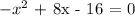
Recall, that the general form of quadratic function is given as

`\text{ ax}^2\text{ + bx + c = 0}`

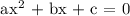
Relating the two functions together

a = -1

b = 8

c = - 16

Determine the number of solutions first using the discriminant

`\begin{gathered} \text{ D = b}^2\text{ - 4ac} \\ \text{ D = \lparen8\rparen}^2\text{ - 4 }*(-1\text{ }*\text{ -16\rparen} \\ \text{ D = 64 - 4\lparen16\rparen} \\ \text{ D= 64 - 64} \\ \text{ D = 0} \end{gathered}`

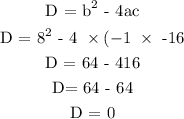
Since D = 0 , then , the quadratic function has one real solution

Solve the equation using the general quadratic formula

`\begin{gathered} \text{ x = }\frac{-b\text{ }\pm\sqrt{b^2\text{ - 4ac}}}{2a} \\ \\ \text{ x = }\frac{-8\text{ }\pm\sqrt{8^2\text{ - 4\lparen-1 }*\text{ -16\rparen}}}{2*-1} \\ \\ \text{ x }=\frac{-8\text{ }\pm\sqrt{64-\text{ 4\lparen16\rparen}}}{-2} \\ \\ \text{ x = }\frac{-8\text{ }\pm\sqrt{64\text{ - 64}}}{-2} \\ \text{ x = }(-8\pm√(0))/(-2) \\ \\ \text{ x = }\frac{-8\pm0}{-2\text{ }} \\ \text{ x }=\text{ }\frac{-8\text{ - 0}}{-2\text{ }}\text{ or }\frac{-8\text{ + 0 }}{-2} \\ \text{ x = 4 or 4} \end{gathered}`

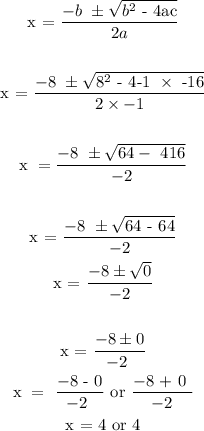
Hence, the value of x is 4