Answer:
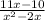
Given:

First, we will find the common denominator for us to be able to subtract the terms:
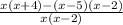
Simplify the expression by performing the operation:
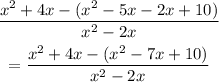
*Distribute the negative sign inside the parenthesis
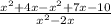
Simplify by adding like terms:
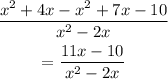
Therefore, the final answer would be:
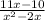
Note:
The -7x and 10 became the opposite signs because we had to distribute the negative sign present before the parenthesis that indicates the subtraction operation.