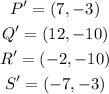Question

Quadrilateral PQRS is transtormed by translating it 6 units to the right and then rotating it’s a 90 degree clockwise about the original. Whitch coordinate pairs represent vertices of p’Q’R’S after these two transformations

Answer 1

Get the coordinates of PQRS, observing the graph, the coordinates are: P = (-3,7), Q = (4,12), R = (4,-2) and S = (-3,-7)

First apply the translation by 6 units to the right. We apply this by adding 6 units to the x values of the points

`\begin{gathered} P=(-3,7)\rightarrow P^(\prime)=(-3+6,7)\rightarrow P^(\prime)=(3,7) \\ Q=(4,12)\rightarrow Q^(\prime)=(4+6,12)\rightarrow Q^(\prime)=(10,12) \\ R=(4,-2)\rightarrow R^(\prime)=(4+6,-2)\rightarrow R^(\prime)=(10,-2) \\ S=(-3,-7)\rightarrow S^(\prime)=(-3+6,-7)\rightarrow S^(\prime)=(3,-7) \end{gathered}`

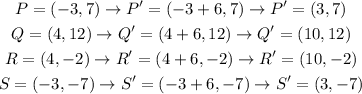
Next apply the rotation transformation which transforms (x , y) into (y , -x)

`\begin{gathered} P^(\prime)=(3,7)\rightarrow P^(\prime)=(7,-3) \\ Q^(\prime)=(10,12)\rightarrow Q^(\prime)=(12,-10) \\ R^(\prime)=(10,-2)\rightarrow R^(\prime)=(-2,-10) \\ S^(\prime)=(3,-7)\rightarrow S^(\prime)=(-7,-3) \end{gathered}`

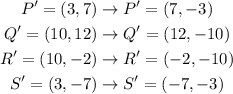
Therefore, the final points for P'Q'R'S' is

`\begin{gathered} P^(\prime)=(7,-3) \\ Q^(\prime)=(12,-10) \\ R^(\prime)=(-2,-10) \\ S^(\prime)=(-7,-3) \end{gathered}`