It says that the given triangle is an isosceles triangle, which means that two of its sides are congruent.
As shown in the figure, the sides across ∠A and ∠C are congruent. This condition must also mean that ∠A and ∠C are congruent.
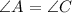
∠C and its adjacent angle measuring 130° are Supplementary, which means that their sum is equal to 180°.
With this, we can get the measure of ∠C.

But,
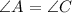
Therefore, ∠A must also be equal to 50°.
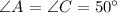
The total sum of all interior angles of a triangle is 180°. With that relationship, we can determine the measure of ∠B since we've already determined the measure of ∠A and ∠C.
We get,
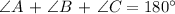

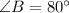
Therefore, ∠A = 50°, ∠B = 50° and ∠C = 80°.