Question

Is this a recursive pattern, a geometric sequence or a arithmetic sequence? Can it be solved? 624262832

Answer 1

Given an a geometric sequence or a arithmetic sequence;

`6,24,26,28,32,\ldots`

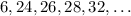
A sequence which follows a regular pattern can be described by a rule, or formula.

`\text{common difference= }(a_(n+1))/(a_n)`

`\begin{gathered} \text{This 6,24,26,28,32, }\ldots \\ \text{This doesn't follow any regular pattern} \end{gathered}`
`\begin{gathered} (24)/(6)=4 \\ \\ (26)/(24)=1.08333 \\ \\ (28)/(28)=1.0769 \\ \\ (32)/(28)=1.4287 \end{gathered}`

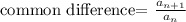
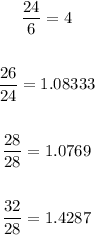
if we find the common difference also, it doesn't follow a regular pattern

`\text{common difference= a}_(n+1)-a_n`
`\begin{gathered} 24-6=18 \\ 26-24=2 \\ 28-26=2 \\ 32-28=4 \end{gathered}`

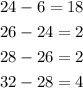
The common difference is not same, Therefore it is not Is this a recursive pattern, a geometric sequence and it is not a arithmetic sequence