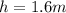Question

find the height of a flagpole which casts a 5.9 M shadow that when the angle of valuation to the sun is 75° round your answer to the nearest tenth

Answer 1

Draw a diagram to visualize the situation:

Notice that φ+θ=90°.

Assuming that the angle φ has a measure of 75°, then:

`\begin{gathered} 75+\theta=90 \\ \Rightarrow\theta=90-75 \\ \Rightarrow\theta=15 \end{gathered}`

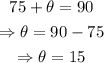
Notice that the flagpole and its shadow are the legs of a right triangle. Recall the definition of the tangent of an angle in a right triangle:

`\tan (A)=\frac{\text{Side opposite to A}}{\text{ Side adjacent to A}}`

Then, in this case:

`\tan (\theta)=(h)/(5.9m)`

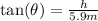
Substitute the value of θ into the equation and isolate h. Then, use a calculator to find the value of h:

`\begin{gathered} h=5.9m*\tan (15) \\ \Rightarrow h=5.9m*0.26795\ldots \\ \Rightarrow h=1.5809\ldots m \end{gathered}`

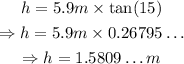
Therefore, to the nearest tenth:

`h=1.6m`