Answer:
6 different ways
Step-by-step explanation:
The girl has a total of 6 colours of thread remaining
Out of the remaining 6 colours left, she needs only 5 threads to complete the tapestry.
This means that she will select 5 out of the available 6 colours of threads to complete the tapestry
This can be done using combination 6C5
Note that:
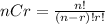
Using the formula above for 6C5
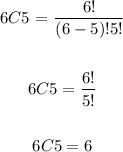
She can finish the tapestry in 6 different ways