Solution
Given the linear equation,
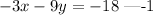
To determine the y-intercept, we need to write it in the form y = mx + c
where m is the gradient and c is the y-intercept.
Adding, 3x to both sides of (1)
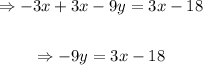
Dividing both sides by -9
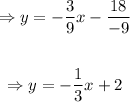
Hence, the y-intercept is 2
To find the x intercept, we equate y = 0 and the find the value of x
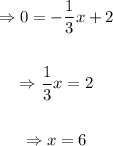
Therefore, the x-intercept is 6.
Knowing the x and y intercept, we can proceed to graph the linear function.