Question

Write a function A that models the amount to which the account grows after T years

Answer 1

item (a):

Using the formula given in the question, we have

`A=P(1+(r)/(n))^(nt)`

Our principal investment P is equal to $4000, our interest r is 3 1/4 %, writting this in decimal form we have

`3(1)/(4)=3+(1)/(4)=3.25`

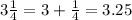
Since it is a percentage, to write in decimal we divide by 100

`(3.25)/(100)=0.0325`

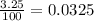
And finally, our n value is 365 since it is compounded daily, and we have 365 days in a year.

Then, our function is

`A(t)=4000(1+(0.0325)/(365))^(365t)_{}`

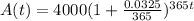
item (b):

To find A(30), we just need to evaluate this value in the function we created before

`A(30)=4000(1+(0.0325)/(365))^(365\cdot30)_{}=10604.2085587\ldots\approx10604.21`

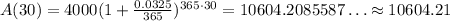
This means that with an investment of $4000, with this rate Joe is going to have a return of $10604.21.