We have to calculate the monthly deposit in order to achieve a certain amount after certain number of years.
The amount is P = $210,000 and the number of years is n = 8 years.
Each deposit will increase a capital that will be compounding the interest, which has a annual rate of r = 10.2%.
As the deposits are made monthly (and we assume this is also the compounding period), we have a number of subperiods m = 12 subperiods per year.
We can use the annuity formula to find the monthly payment M so as to have a future value of FV = 210000:
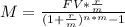
We can replace with the values and calculate the amount as:
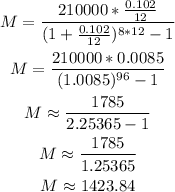
2) We have to calculate how much they deposit into the account.
As they deposit monthly during 8 years, the amount of deposits will be 12*8 = 96 deposits.
We can then multiply by the deposit amount and obtain:
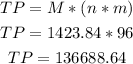
Answer:
1) Monthly payment = $1,423.84
2) $136,688.64