Question

2) Keira wants to make an open-top box by cutting out corners of a square piece of cardboard andfolding up the sides. The cardboard is 12 centimeters by 12 centimeters. The volume V(x) incubic centimeters of the open-top box is a function of the side length x in centimeters of thesquare cutouts.a) Write an expression for V(x).b) What is the volume of the box when x = 4?c) What is a reasonable domain for the Volume in this context?yes

Answer 1

Keira wants to make the open-top box as described in the problem.

The card box is 12 x 12 centimeters. Keira will cut 4 corners of side x and fold up the sides.

This means the base of the box is (12-2x) by (12-2x) and the height of the box is x.

Thus, the volume of the box is:

V = (12-2x)(12-2x)x

a) To write an expression for V(x), we'll multiply the expression in parentheses:

`\begin{gathered} V\mleft(x\mright)=(144-24x-24x+4x^2)x \\ \text{Simplifying:} \\ V(x)=(144-48x+4x^2)x \end{gathered}`

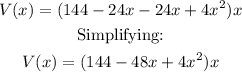
Now multiply the last term:

`V(x)=144x-48x^2+4x^3`

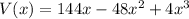
This is the required expression for V(x)

b) The volume of the box for x=4 is calculated by substituting the value into the expression above:

`\begin{gathered} V(4)=144(4)-48(16)+4(64) \\ \text{Calculating:} \\ V(4)=64 \end{gathered}`

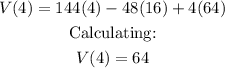
The volume is 64 cubic centimeters

c) To find a reasonable domain for V(x), we'll return to the first expression:

V = (12-2x)(12-2x)x

The domain can be obtained by assuming the volume cannot be negative. Neither of the sides of the box can be negative, so the conditions that define the domain are:

12 - 2x > 0

and

x > 0

The first condition results in:

x < 6

Thus, the domain of the Volume function is all the numbers greater than 0 and less than 6, or: (0,6)

If the volume is allowed to be zero, then the endpoints are included: [0,6]