Question

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.Match the equation of a parabola to its focus and directrix

Answer 1

For the given question, we will find the equation of the parabola of each box

then, we will select the correct equation from the tiles

The first box: focus (2, -2) and directrix y = -8

So, the parabola will open up and the equation will be:

`\begin{gathered} h=2;k=(-8+(-2))/(2)=-5 \\ (x-h)^2=4\cdot a(y-k) \\ a=3 \\ \\ (x-2)^2=12\cdot(y+5) \end{gathered}`

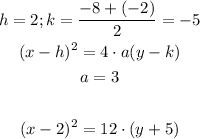
simplify the equation

`\begin{gathered} x^2-4x+4=12y+60 \\ y=(x^2)/(12)-(x)/(3)-(14)/(3) \end{gathered}`

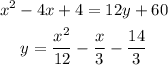
The second box: Focus (-3, 6) and Directrix (x = -11)

So, the parabola will open right

The values of (a) and the vertex (h,k) will be:

`\begin{gathered} a=(-3-(-11))/(2)=(-3+11)/(2)=(8)/(2)=4 \\ \\ h=(-3+(-11))/(2)=-7;k=6 \end{gathered}`

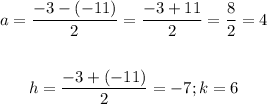
The equation of the parabola will be:

`\begin{gathered} (y-k)^2=4a(x-h) \\ (y-6)^2=4\cdot4(x+7) \end{gathered}`

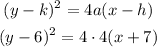
Simplifying the equation:

`\begin{gathered} y^2-12y+36=16x+112 \\ x=(y^2)/(16)-(3y)/(4)-(19)/(4) \end{gathered}`

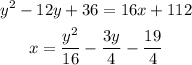
The third box: Focus (2, -2); Directrix (x = 8)

So, the parabola will open left

The values of (a) and the vertex (h,k) will be:

`\begin{gathered} a=(8-2)/(2)=(6)/(2)=3 \\ h=(8+2)/(2)=5;k=-2 \end{gathered}`

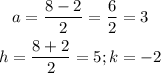
The equation of the parabola will be:

`\begin{gathered} (y-k)^2=-4a(x-h) \\ (y+2)^2=-12(x-5) \\ \end{gathered}`

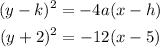
Simplifying the equation:

`\begin{gathered} y^2+4y+4=-12x+60 \\ x=-(y^2)/(12)-(y)/(3)+(14)/(3) \end{gathered}`

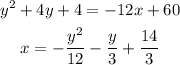
The fourth box: Focus (-7, 1) and Directrix (y = 11)

The parabola will open down

The values of (a) and the vertex (h,k) will be:

`\begin{gathered} a=(11-1)/(2)=(10)/(2)=5 \\ h=-7;k=(11+1)/(2)=(12)/(2)=6 \end{gathered}`

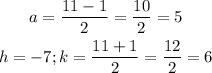
The equation of the parabola will be:

`\begin{gathered} (x-h)^2=-4a(y-k) \\ (x+7)^2=-20(y-6) \end{gathered}`

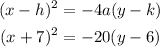
Simplifying the equation:

`\begin{gathered} x^2+14x+49=-20y+120 \\ \\ y=-(x^2)/(20)-(7x)/(10)+(71)/(20) \end{gathered}`

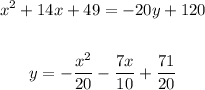
The drag of the tiles to the boxes according to the following figure: