Question

A solid has volume 2 cubic units and surface area 10 square units. The solid is dilated, and the image has volume 128 cubic units. What is the surface area of the new solid?

Answer 1

In this type of problem. You need to determine first the unit dimension..

The dimension of the volume is in cubic so the unit dimension will be the cube root the volume:

Let u = unit dimension

`u=\sqrt[3]{V}`

So we now have the unit dimension, dilating it with a scale factor of k will give as a new volume. Since it is a unit dimension, you need to take the cube of it so you will arrive with the new volume.

So the new volume will be :

`V_{\text{new}}=(uk)^3`

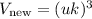
or just simply :

`V_{\text{new}}=(k\sqrt[^{}3]{V})^3`
`k=\frac{\sqrt[3]{V_{\text{new}}}}{\sqrt[3]{V}}=\sqrt[3]{(V_(new))/(V)}`

Solving for the scale factor k :

`k=\sqrt[3]{(128)/(2)}=\sqrt[3]{64}=4`

So now we have the scale factor of k = 4

Now for the Surface Area , the dimension of it is in square units, so the unit dimension will be the square root of the surface area :

It has almost the same formula for k, but the difference is only the cube root or the square root.

So we can state that the New surface area will be :

`SA_{\text{new}}=(k\sqrt[]{SA})^2`

Solving for the New surface area :

`SA_{\text{new}}=(4\sqrt[]{10})^2=160`

So the answer is 160 square units.