Question

A line passes through the points (5, 12) and (4, 10). Find this line's equation in point-slope form. Using the point (5, 12)this line's point-slope form equation is [ ]Using the point (4, 10) this line's point-slope form equation is [ ]

Answer 1

We have to write the point-slope form equation of a line that pass through points (5,12) and (4,10).

The point-slope form can be written as:

`y-y_0=m(x-x_0)`

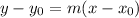
where (x0,y0) are the coordinates of any point in the line and m is the slope of the line.

Then, we can start by calculating the slope of the line as:

`m=(y_2-y_1)/(x_2-x_1)=(10-12)/(4-5)=(-2)/(-1)=2`

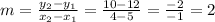
The slope-point equation for the line can be written differently depending on the point selected.

Using the point (5, 12) this line's point-slope form equation is:

`y-12=2(x-5)`

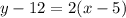
Using the point (4, 10) this line's point-slope form equation is:

`y-10=2(x-4)`

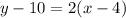
Answer:

Using the point (5, 12) this line's point-slope form equation is: y-12=2(x-5).

Using the point (4, 10) this line's point-slope form equation is: y-10=2(x-4).