Question

How many miles will be remaining after 59 minutes of driving

Answer 1

The graph depicts a linear relationship between her driving time (x variable) and the remaining distance (y variable). Knowing that this is a linear relationship, we can represent it as a equation in the slope intercept form. This is because we already have the slope as -0.9.

Therefore we would have the following;

`\begin{gathered} y=mx+b \\ \text{Where;} \\ x=47,y=41,m=-0.9 \end{gathered}`

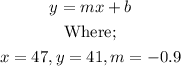
We can now substitute the given variables into the equation in slope-intercept form as follows;

`\begin{gathered} y=mx+b \\ 41=-0.9(47)+b \\ 41=-42.3+b \\ \text{Add 42.3 to both sides;} \\ 41+42.3=-42.3+42.3+b \\ 83.3=b \\ \text{The equation therefore becomes;} \\ y=-0.9x+83.3 \end{gathered}`

With the equation for the graph now determined, we shall find the mileage after 59 minutes of driving as follows;

`\begin{gathered} \text{After 53 minutes of driving (x),} \\ \text{The miles remaining (y) shall be;} \\ y=-0.9x+83.3 \\ y=-0.9(53)+83.3 \\ y=-47.7+83.3 \\ y=35.6 \end{gathered}`

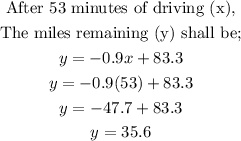
ANSWER:

After 59 minutes of driving, she would have 35.6 miles remaining.