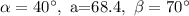Question

Solve the triangle: b = 100, c = 100, y = 70". If it is not possible, say so.This triangle is not solvable.Q = 70', a = 68.4, B = 40"Q = 40", a = 100, B= 70"Q = 40", a = 68.4, B= 70'

Answer 1

Given:

`\begin{gathered} b=100 \\ c=100 \\ \gamma=70^(\circ) \end{gathered}`

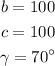
Since two sides are equal, the triangle must be an isosceles triangle.

Using the law of sines,

`\begin{gathered} (\sin\gamma)/(c)=(\sin\beta)/(b) \\ (\sin 70^(\circ))/(100)=(\sin\beta)/(100) \\ \sin \beta=\sin 70^(\circ) \\ \beta=\sin ^(-1)(\sin 70^(\circ)) \\ \beta=70^(\circ) \end{gathered}`

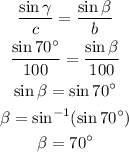
Since the angles opposite to equal sides are equal, the triangle is isosceles and hence solvable.

The third angle of the triangle is,

`\begin{gathered} \alpha=180^(\circ)-\beta-\gamma \\ =180^(\circ)-70^(\circ)-70^(\circ) \\ =40^(\circ) \end{gathered}`

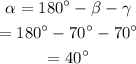
Now, using the law of sines,

`\begin{gathered} (\sin\alpha)/(a)=(\sin \beta)/(b) \\ (\sin 40^(\circ))/(a)=(\sin 70^(\circ))/(100) \\ a=(\sin 40^(\circ))/(\sin 70^(\circ))*100 \\ a=68.4 \end{gathered}`

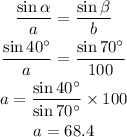
Therefore, the solution of the triangle is,

`\alpha=40^(\circ),\text{ a=68.4},\text{ }\beta=70^(\circ)`