Question

The following is true about similar triangles DOT and ANG. DO AN OT NG DT AG 3 3 1 Which could be the length of DT and AG?

Answer 1

DT=6 and AG=2

C

Step-by-step explanation:

Given that the Triangle DOT and ANG are similar.

The ratio of their corresponding sides will be equal;

`(DO)/(AN)=(OT)/(NG)=(DT)/(AG)=(3)/(1)`

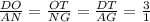
So, according to the given ratio, the ratio of the corresponding sides of triangle DOT to ANG is equal to 3/1.

From the given options, the correct option is the one whose ratio is equal to 3/1;

`(DT)/(AG)=(3)/(1)`
`\begin{gathered} A\text{.} \\ (9)/(6)\\e(3)/(1) \end{gathered}`
`\begin{gathered} B\text{.} \\ (6)/(4)\\e(3)/(1) \end{gathered}`
`\begin{gathered} C\text{.} \\ (6)/(2)=(3)/(1) \end{gathered}`
`\begin{gathered} D\text{.} \\ (9)/(4)\\e(3)/(1) \end{gathered}`

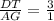
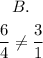
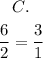
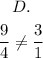
Therefore, the only option whose ratio of side DT to AG is equal to 3/1 is C;

DT=6 and AG=2