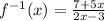Question

when is f(x) increasing and/or decreasingwhat is the inverse of f(x)? is it a function? what's the reasoning for it?f(x)=(3x+7)/(2x-5)

Answer 1

In order to determine when the function is increasing or decresaing, we shall begin by taking its derivative, as follows;

`\begin{gathered} f(x)=(3x+7)/(2x-5) \\ y^(\prime)=((2x-5)-(3x+7))/((2x-5)^2) \\ We\text{ simplify and we now have;} \\ y^(\prime)=(2x-5-3x-7)/((2x-5)^2) \\ y^(\prime)=(-x-12)/((2x-5)^2) \end{gathered}`

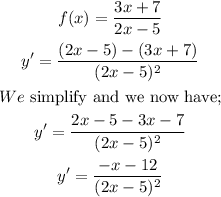
The numerator of the derivative is negative. When the result is a negative that means the function is decreasing.

Also, the inverse of the function f(x) is derived as follows;

`\begin{gathered} f(x)=((3x+7))/((2x-5)) \\ We\text{ re-write this as an equation as follows;} \\ y=(3x+7)/(2x-5) \\ We\text{ now switch places for variables x and y;} \\ x=(3y+7)/(2y-5) \\ \text{Cross multiply and you'll have;} \\ x(2y-5)=3y+7 \\ 2xy-5x=3y+7 \\ \text{Subtract 3y from both sides;} \\ 2xy-5x-3y=7 \\ \text{Add 5x to both sides;} \\ 2xy-3y=7+5x \\ \text{Factor out y from the left side;} \\ y(2x-3)=7+5x \\ \text{Divide both sides by }(2x-3) \\ y=((7+5x))/((2x-3)) \\ We\text{ can now re-write this using function notation} \\ f^(-1)(x)=((7+5x))/((2x-3)) \end{gathered}`

ANSWER:

The function f(x) is decreasing at the point of discontinuity (when the function is undefined) which is

`\begin{gathered} 2x-5=0 \\ 2x=5 \\ x=(5)/(2) \\ x=2.5 \end{gathered}`

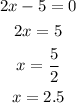
The inverse of the function is;

`f^(-1)(x)=(7+5x)/(2x-3)`