The given inequality is
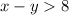
The given coordinates are (7,4), (3.8, 4) and (0,9).
Let's evaluate each coordinated pair in the inequality to see which one satisfies it.
For (7,4).
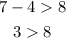
Since 3 is not more than 8, we say (7,4) is not a solution.
For (3.8, 4).
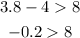
Since -0.2 is not more than 8, we say (3.8, 4) is not a solution.
For (0,9).
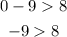
Since -9 is not more than 8, we say (0,9) is not a solution.
Therefore, neither given point is a solution of the given inequality.