Question

Question 1: 11 ptsBased on results from recent track meets, Denita has a 68% chance of getting a medal in the 100 meter dash. Estimate the probability that Denita will get a medalin at least 5 of the next 10 races. Use the random number table, and make at least 10 trials for your simulation. Express your answer as a percent.

Answer 1

According to the binomial distribution of probability

`P(k;n,p)=P(X=k)=(nbinomialk)p^k(1-p)^(n-k)`

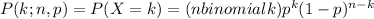
In our case,

`n=10,p=68\text{percent}=0.68`

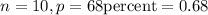
Therefore,

`P(k\ge5)=\sum ^(10)_(k=5)(10binomialk)(0.68)^k(1-0.68)^(10-k)`

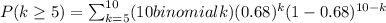
Thus,

`\Rightarrow P(k\ge5)=(10binomial5)(0.68)^5(0.32)^5+(10binomial6)(0.68)^6(0.32)^4+(10binomial7)(0.68)^7(0.32)^3+(10binomial8)(0.68)^8(0.32)^2+(10binomial9)(0.68)^9(0.32)^1+(10binomial10)(0.68)^(10)(0.32)^0`

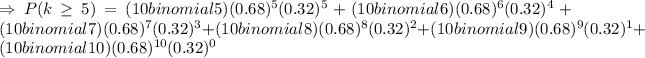
After calculations, we reach the following result

`\Rightarrow P(k\ge5)=0.9362\ldots`

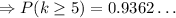
Then, the probability of Denita winning a medal in at least 5 of the next 10 races is, approximately 93.63%. The close option is 100%