Question

The height of a triangle is three more than two times the base. The area of the triangle is 45 square feet. What are the dimensions of the triangle? (solved by factoring)

Answer 1

Given the question in the tab, the following are the solution steps to answer the question.

STEP 1: Write the given data

`\begin{gathered} Area=45ft^2 \\ 2\text{ times the base \lparen b\rparen}\Rightarrow2b \\ three\text{ more than two times the base \lparen b\rparen}\Rightarrow2b+3 \\ height(h)=2b+3 \end{gathered}`

STEP 2: Write the formula for the are of a triangle

`Area=(1)/(2)* base* height`

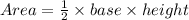
STEP 3: Substitute the given values

`\begin{gathered} Area=(1)/(2)* b* h=45ft^2 \\ By\text{ substitution,} \\ (1)/(2)* b* h=(bh)/(2) \\ Recall\text{ from step 1 that:} \\ h=2b+3 \\ By\text{ substitution,} \\ Area=(b(2b+3))/(2)=45 \end{gathered}`

STEP 4: Cross multiply

`\begin{gathered} b(2b+3)=2*45 \\ b(2b+3)=90 \end{gathered}`

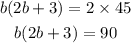
Open the bracket

`2b^2+3b=90`

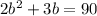
Subtract 90 from both sides

`2b^2+3b-90=0`

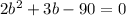
STEP 5: Solve the derived equations using quadratic formula

`\begin{gathered} b_1,b_2=(-b\pm√(b^2-4ac))/(2a) \\ a=2,b=3,c=-90 \\ By\text{ substitution,} \\ b_(1,\:2)=(-3\pm √(3^2-4\cdot \:2\left(-90\right)))/(2\cdot \:2) \\ √(3^2-4*2(-90))=√(9+720)=√(729)=27 \\ \\ \text{By substitution, we have:} \\ b_(1,\:2)=(-3\pm \:27)/(2\cdot \:2) \\ \mathrm{Separate\:the\:solutions} \\ b_1=(-3+27)/(2\cdot\:2)=(24)/(4)=6 \\ b_2=(-3-27)/(2\cdot\:2)=(-30)/(4)=-7.5 \\ \\ \therefore base=-7.5,6 \end{gathered}`

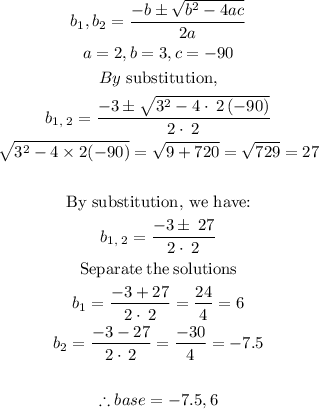
Since the value of the base of a triangle can not be negative, the base of the triangle is 6ft

STEP 6: Find the value of the height

`\begin{gathered} From\text{ step 3} \\ h=2b+3 \\ b=6ft \\ h=2(6)+3=12+3=15ft \end{gathered}`

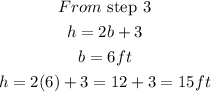
Hence, the dimension of the triangle are:

base = 6ft

height = 15ft