Question

I need help with these questions. Please help and please explain step-by-step explanation

1. Find the value of c that gives the function the given minimum value.

f (x) = 4x^2+ 12x + c; minimum value -5
A40
B-40
C c=-14
D c=4

Find the value of b that gives the function the given maximum value.

f (x) = -x^2 + bx + 7; maximum value 11
A b=7
B b=7, b=-7
C b=-4 or b=4
D b=4

Answer 1

D) c = 4

C) b = -4 or b = 4

Explanation:

The minimum/maximum value of a quadratic function is the y-coordinate of the function's vertex.

The x-coordinate of a function's vertex can be found using the following formula:

`\textsf{$x$-coordinate of the vertex}=-(b)/(2a)\quad \textsf{(for $ax^2+bx+c$)}.`

-----------------------------------------------------------------------------------------------

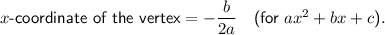
Given function:

`f (x) = 4x^2+ 12x + c`

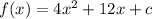
Therefore,

`\textsf{$x$-coordinate of the vertex}=-(b)/(2a)=-(12)/(2(4))=-1.5`

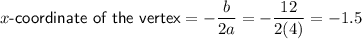
Substitute the found x-value of the vertex into the function, equate it to -5, then solve for c:

`\begin{aligned} f(-1.5)&=-5\\\implies4(-1.5)^2+12(-1.5)+c&=-5\\4(2.25)-18+c&=-5\\9-18+c&=-5\\-9+c&=-5\\c&=4\end{aligned}`

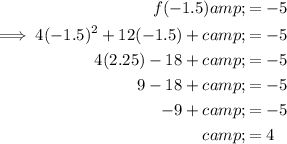
Therefore, c = 4.

-----------------------------------------------------------------------------------------------

Given function:

`f (x) = -x^2 + bx + 7`

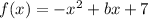
Therefore,

`\textsf{$x$-coordinate of the vertex}=-(b)/(2(-1))=0.5b`

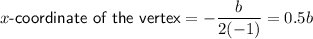
Substitute the found x-value of the vertex into the function, equate it to 11, then solve for b:

`\begin{aligned} f(0.5b)&=11\\\implies-(0.5b)^2+b(0.5b)+7&=11\\-0.25b^2+0.5b^2+7&=11\\0.25b^2&=4\\b^2&=16\\√(b^2)&=√(16)\\b&=\pm4\end{aligned}`

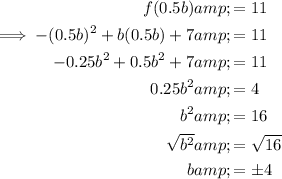
Therefore, b = -4 or b = 4.