Given that a retailer needs to purchase 12 printers, the first printer cost $54.
It is known that each additional printer costs 5% less than than the cost of the previous printer.
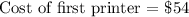
Cost of the second printer
The second printer costs 5% less than the first printer, we thus have
Cost of the third printer
The third printer costs 5% less than the second printer, we thus have

Cost of the fourth printer
The fourth printer costs 5% less than the third printer, we thus have

Cost of the fifth printer
The fifth printer costs 5% less than the fourth printer, we thus have

Cost of the sixth printer
The sixth printer costs 5% less than the fifth printer, we thus have

Cost of the seventh printer
The seventh printer costs 5% less than the sixth printer, we thus have

Cost of the eighth printer
The eighth printer costs 5% less than the seventh printer, we thus have

Cost of the ninth printer
The ninth printer costs 5% less than the eighth printer, we thus have

Cost of the tenth printer
The tenth printer costs 5% less than the ninth printer, we thus have

Cost of the eleventh printer
The eleventh printer costs 5% less than the tenth printer, we thus have
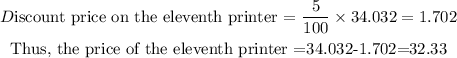
Cost of the twelfth printer
The twelfth printer costs 5% less than the eleventh printer, we thus have

Thus, the total cost of 12 printers is evaluated as
![\begin{gathered} 54+51.3+48.735+46.298+43.981+41.782+39.693+37.708+35.823+34.032+32.33+30.713_{_{_{}}} \\ =496.4 \end{gathered}]()
Thus, the sum of twelve printers is $496.4
The second option is the correct answer.