Question

Suppose that there are two types of tickets to a show: advance and same-day. Advance tickets cost $15 and same-day tickets cost $20. For one performance,there were 45 tickets sold in all, and the total amount paid for them was $825. How many tickets of each type were sold?Number of advance tickets sold: Number of same-day tickets sold:

Answer 1

Let,

Number of Advance Tickets = a

Number of Same-Day tickets = s

Given,

Total 45 tickets sold

We can write

`a+s=45`

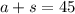
Also, each advance ticket cost $15 and same day tickets cost $20 for a total of $825. Thus, we can write:

`15a+20s=825`

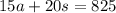
We will multiply the first equation by - 15 and then add both equations. Then, solve for "s". The steps are shown below:

`\begin{gathered} -15*\lbrack a+s=45\rbrack \\ -15a-15s=-675 \\ ------------- \\ -15a-15s=-675 \\ 15a+20s=825 \\ ------------- \\ 5s=150 \\ s=(150)/(5) \\ s=30 \end{gathered}`

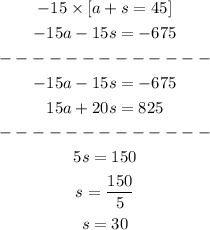
Now, we can use this value of "s" and put it into Equation 1 and find the value of "a". Shown below:

`\begin{gathered} a+s=45 \\ a+30=45 \\ a=45-30 \\ a=15 \end{gathered}`

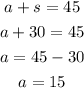
Answer

Number of advance tickets sold: 15

Number of same-day tickets sold: 30