In order to graph the parabola, first let's identify the x-coordinate of the vertex.
To do so, we can use the formula below, after identifying the parameters a, b and c from the standard form of the equation:
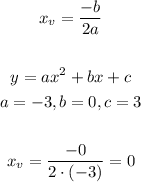
Now, let's calculate the points using x = -2, x = -1, x = 0, x = 1 and x = 2:
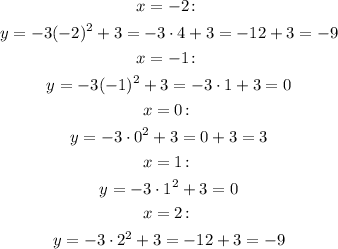
Graphing these points and the corresponding parabola, we have: