The standard derivation of the sample (s) is:
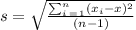
Where:
s = standard derivation of sample
n = number of data provided
xi = each of the values of the sample
x = the mean of xi
So, first, let's find the mean.
Given:
n = 6
The mean is:
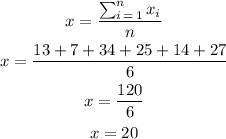
And the standard derivation:
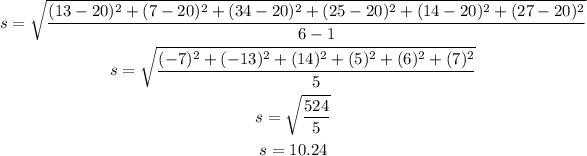
Answer: 10.24.