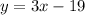Hello!
We know that:
• Slope ,= 3
,
• The, line passes through the point, (7, 2)
Knowing it, let's answer your exercise:
What is the point-slope of the equation of the line?
First, we have to remember how to write the point-slope equation:
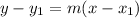
As we know the values, we just have to replace them:
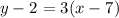
What is the slope-intercept form of the equation of the line?
The slope-intercept form is:

We have to calculate the y-intercept (b). So, let's do it by replacing the point and slope in the variables:
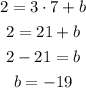
So, the slope-intercept form is: