ANSWER
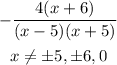
Step-by-step explanation
We want to simplify the expression:
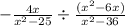
To do this, first change the sign to a multiplication sign and flip the fraction on the right:
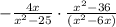
Now, simplify the expression by applying the difference of two squares and factorization:
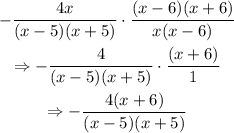
The expression will be invalid when x is:
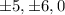
Therefore, the answer is option C.