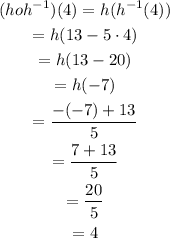Question

The one-to-one functions g and h are defined as follows.g={(-9, 8), (2, 9), (4, 7), (5, 2), (6, -9)}-X+13h(x) =5

Answer 1

In order to calculate g^-1(-9), since it's an inverse function, we just need to find the value of x for y = -9.

Looking at the set of points of g, we can see that for y = -9 we have x = 6, so:

`g^(-1)(-9)=6`

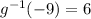
Then, to find h^-1(x), let's change h(x) by x and x by h^-1(x) in the function:

`\begin{gathered} h(x)=(-x+13)/(5) \\ x=(-h^(-1)(x)+13)/(5) \\ -h^(-1)(x)+13=5x_{}_{} \\ -h^(-1)(x)=5x-13 \\ h^(-1)(x)=13-5x \end{gathered}`

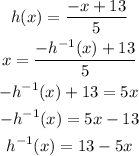
Finally, calculating (h o h^-1)(4), that is, the composite function h of h^-1 of 4 we have:

`\begin{gathered} (hoh^(-1))(4)=h(h^(-1)(4)) \\ =h(13-5\cdot4) \\ =h(13-20) \\ =h(-7) \\ =(-(-7)+13)/(5) \\ =(7+13)/(5) \\ =(20)/(5) \\ =4 \end{gathered}`