Answer: -17
=====================================================
Step-by-step explanation:
Plug in x = 1 which is the left endpoint of the interval [1,5] aka

g(x)=-3x^2+x+1
g(1)=-3(1)^2+1+1
g(1) = -1
Then plug in x = 5 which is the right endpoint of that interval mentioned.
g(x) = -3x^2+x+1
g(5) = -3(5)^2+5+1
g(5) = -69
---------
AROC = average rate of change
The AROC of g(x) from x = a to x = b is given by this formula
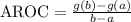
Plug in a = 1 and b = 5. Then simplify.
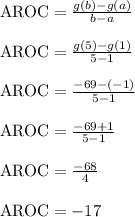
The average rate of change on the interval [1, 5] is -17
This is the same as finding the slope through the lines (1,-1) and (5,-69). Notice the form and structure of the AROC formula mimics the slope formula.
The g(b)-g(a) portion mimics y2-y1 in the numerator.
The b-a portion mimics x2-x1 in the denominator.