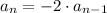Question

Write a recursive sequence that represents the sequence defined by the following explicit formula: an = = -4(-2)^n

Answer 1

In order to find the sequence represented by the given explicit

formula we have to plug in the values of n.

The formula is

`a_n=-4(-2)^n`

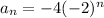
hence, for n=1, we have

`a_1=-4(-2)^1`

which is equal to

`\begin{gathered} a_1=-4(-2)^{} \\ a_1=8 \end{gathered}`

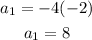
In the same way, for n=2, we have

`\begin{gathered} a_2=-4(-2)^2 \\ a_2=-4(4) \\ a_2=-16 \end{gathered}`

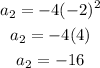
For n=3, it yields

`\begin{gathered} a_3=-4(-2)^3 \\ a_3=-4(-8) \\ a_3=32 \end{gathered}`

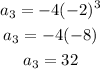
For n=4, we obtain

`\begin{gathered} a_4=-4(-2)^4 \\ a_4=-4(16) \\ a_4=-64 \end{gathered}`

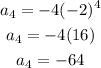
and so on.

Now,

`\begin{gathered} a_(n-1)=-4(-2)^(n-1) \\ a_(n-1)=-4(-2)^n(-2)^(-1) \\ a_(n-1)=\frac{-4(-2^{})^n}{-2} \\ -2\cdot a_(n-1)=-4(-2)^n \end{gathered}`

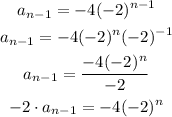
since, we know that

`\begin{gathered} a_n=-4(-2)^n \\ we\text{ have } \\ -2\cdot a_(n-1)=a_n \end{gathered}`

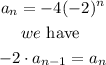
in other words, we have that

`a_n=-2\cdot a_(n-1)`