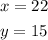
Step-by-step explanation
Step 1
when a lines intersects a pair of parallel lines , diverse angles are created
All angles that are either exterior angles, interior angles, alternate angles or corresponding angles are all congruent,so ( in the image yellow angles are corresponding, so)
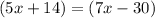
solve for x

Step 2
now, yellow angle and ble angles are supplementary( Two Angles are Supplementary when they add up to 180 degrees),so
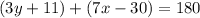
let
x=22
and solve for y

I hope this helps you