Since the path of Grant is a line segment, the first step to solve the exercise is to find the slope of the line segment. For this, we can use the following formula:

As we can see in the graph, the line segment passes through the points (8,0) and (-4,6). Then, we have:
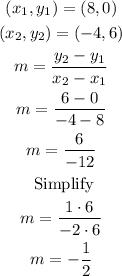
Now that we have the slope of the line segment and a point which it passes, we can use the point-slope formula:
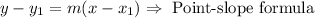
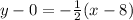
Finally, we solve for y the above equation:

Therefore, the equation that represents the path of Grant is:
