Given the arithmetic sequence in the question, we can deduce that the common difference, d, is 4 and the first term, a1, is 4. The below formula will be used to solve for the 60th term of the sequence;

Where a1 = first term = 4
d = common difference = 4
n = number of term = 60
Let's go ahead and substitute the given values into our equation;
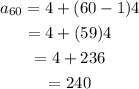
Therefore, the 60th term of the sequence is 240.