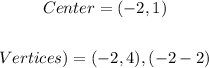Step-by-step explanation:
Given;
We are given the following equation of an ellipse;
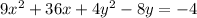
Required;
We are required to graph the ellipse and state its center and vertices.
Step-by-step solution;
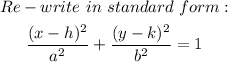
We now have;
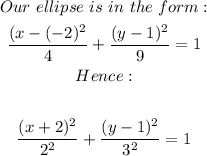
With the center given as (h, k), we now have

Also,
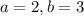
Using a graphing tool, the graph would now appear as follows;
The vertices as shown in the graph are found at the point;

Therefore,
ANSWER: