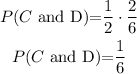Question

A coin is flipped and a normal 6 sided die is rolled find the probability of getting a head on the coin and a number greater than 4 on the die

Answer 1

`P(C\text{ and D)=}(1)/(6)`

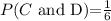
Explanation:

Probability is represented by the following equation:

`P(A)=\frac{\text{Number of favorable outcomes}}{\text{Total number of favorable outcomes}}`

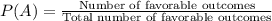
Therefore, for this situation:

`\begin{gathered} P(\text{Coin)}=(1)/(2) \\ P(\text{Die)}=(2)/(6) \end{gathered}`

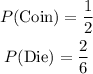
Since the probability of two events occurring together but independents is represented by the multiplication of the probabilities of the events:

`\begin{gathered} P(C\text{ and D)=}(1)/(2)\cdot(2)/(6) \\ P(C\text{ and D)=}(1)/(6) \end{gathered}`