Answer:
• The scale factor of the volume of the bags is 20.
,
• The scale factor of the dimensions of the two bags is 2.7
,
• The scale factor of the surface areas of the two bags is 7.4
Explanation:
Given:
• The volume of the small bag = 2 pounds.
,
• The volume of the large bag = 40 pounds.
We want to determine the ratio by which the surface area of the small bag increases.
First, given the side lengths of two solids:
• The, ratio of the surface areas, of the two solids is ,the ratio of the square of the side lengths,.
,
• The, ratio of the volume, of the two solids is ,the ratio of the cubes of the side lengths,.
Let the side lengths of the large and small bag be x and y respectively.
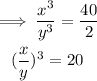
The scale factor of the volume of the bags is 20.
Next, find the ratio of the side lengths by taking the cube root of both sides.
![(x)/(y)=\sqrt[3]{20}=2.7](https://img.qammunity.org/2023/formulas/mathematics/high-school/ztd4mmlcw7buv7x9acuo9izdseibpjr4j2.png)
The scale factor of the dimensions of the two bags is 2.7
Therefore, the ratio of the surface areas will be:
![((x)/(y))^2=(\sqrt[3]{20})^2=7.4](https://img.qammunity.org/2023/formulas/mathematics/high-school/9a3p9el80stvjq2p7x1aohv1vsqlosux7u.png)
The scale factor of the surface areas of the two bags is 7.4