Question

The speed of transverse waves along a stretched spring is 6.18 meters per second. The spring is 4.02 meters long and is held in place at both ends. What are the first three natural frequencies of the spring? Include units in your answers.

Answer 1

The speed v of a transverse wave is related to its wavelength λ and its frequency f by the equation:

`v=\lambda f`

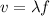
When a string or any string-like object (like the stretched spring) vibrates at its fundamental frequency f₁, the wavelength of the standing wave is equal to 2 times the length of the string:

`\lambda=2L`

Then:

`v=2Lf_1`

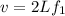
Isolate the fundamental frequency from the equation:

`f_1=(v)/(2L)`

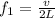
The n-th natural frequency is given as a multiple of the fundamental frequency:

`f_n=n* f_1`

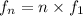
Then, to find the first three natural frequencies, find the value of the fundamental frequency by replacing the speed of the transverse wave v=6.18m/s and the length of the stretched spring L=4.02m:

`f_1=(6.18(m)/(s))/(2*4.02m)=0.7686567\ldots Hz`

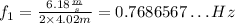
Then, the next two natural frequencies are:

`\begin{gathered} f_2=2* f_1=2*(0.7686567\ldots Hz)=1.5373\ldots Hz \\ \\ f_3=3* f_1=3*(0.7686567\ldots Hz)=2.30597\ldots Hz \end{gathered}`

Therefore, the first three natural frequencies of the spring are approximately 0.769Hz, 1.54Hz and 2.31Hz.